Writing tests with high coverage is almost always tedious work that is still error prone. This can lead to missing crucial details that cause undesirable behavior, and, in the worst case, a complete system failure. What if there were an efficient way to automate this work?

In my research, I investigate how to automate testing through a systematic exploration of all admissible program inputs. The technique I have developed is called compilation-based abstraction. In this technique, the program under test is transformed to compute with a set of input values instead of a single value. This allows exploration of multiple program inputs (possibly all) at once, hence providing higher guarantees than just pure testing.

How to trust your code?

In general, to gain trust in your code, you write tests that simulate interactions with the environment; that is, you capture concrete scenarios with encoded input values. Alternatively, you can deploy more sophisticated analyses, like fuzzing or randomized testing. However, the reliability of these techniques is influenced by a human factor. The developer might always miss some test cases or omit some properties of the code entirely.

The natural way to mitigate the human factor is automation. Generating test cases automatically is an appealing solution; however, examining all possible program interactions presents a problem. If we would like to explore all possibilities naively, even for a simple program that only takes a single integer as an input value, that would already make 2,147,483,647 possible executions to explore. However, many of those executions take the same path. In automation, we would like to generalize them. In fact, developers also apply a similar process when they design test case scenarios.

Examine the artificial program in Figure 1.
Can you guess for which values of a and b the assert (post-condition of the procedure) will be triggered?

1 void procedure() {
2  int a = input();
3  int b = input();
4  int x = 1, y = 0;
5  if (a > 0) {
6    y = x + 3;
7    if (b == 0)
8      x = 2 * (a + b);
9  }
10  assert(x – y != 0);
11 }

Figure 1. Artificial program

Examining all possible inputs is indeed unnecessary. We may recognize that there are only a few classes of inputs in which the program behaves differently. For example, for all negative inputs of variable a, the procedure’s behavior is always the same because, in all executions, we perform the same instructions (we do not execute the code inside the block of the first condition).

For efficient automation of exhaustive testing, we want to find a way to describe these classes efficiently and perform computation with them. One such technique that allows us to compute with sets of values is symbolic execution.

Symbolic execution

Symbolic execution is a program analysis based on the same idea as testing: it executes paths in a given program to find bugs. However, symbolic execution and testing differ in how they actually execute program paths. In testing, we execute a given program for each input in a given set. This means that the program is passed many inputs during testing, and for each input, the corresponding execution follows exactly one program path. On the other hand, in symbolic execution, the program is passed only one input. This single input does not consist of concrete data (like numbers or strings); rather, it is represented by symbols (names of inputs). These symbols represent any concrete input data we can possibly pass to the program. The program is then executed with these symbols. Individual program statements generally manipulate expressions containing symbols instead of performing common calculations with numbers.

Figure 2 shows all possible paths of symbolic execution of the program from the previous example. Boxes describe values of variables at each program location. Each location also contains a so-called path-condition π that keeps all the constraints on the symbolic values. The symbolic values used in the example are α and β.

Notably, symbolic execution gives us the following guarantees:

It executes only truly executable program paths, i.e., those which can be followed for some concrete input by standard execution.

Each executable path is symbolically executed at most once.

For a symbolically executed program path, we can directly compute a representative concrete input for which standard execution will follow exactly that path.

Even though the symbolic execution technique seems promising, there are scenarios in which it is too slow to be of any use. This is caused by expensive computation with symbolic expressions and a so-called path explosion problem, i.e., when an enormous number of paths is generated during the execution. To mitigate these problems, we can leverage techniques like abstract execution (interpretation), but we pay the cost of analysis precision (coverage).  In comparison to symbolic execution, the abstract execution does not compute with symbols but rather with an abstract representation of values.

Abstract representation describes only some properties about values, for example, whether the value can be a null pointer, signed integer, or a particular form of string. We gain execution performance by abstracting only specific properties, since a single abstract path might describe multiple symbolic paths. However, this is in trade for the precision of analysis. By keeping track of only specific properties, we might omit some paths that lead to an error location, which we call underapproximating abstraction. Or, in the case of overapproximating abstraction, we might find an error that is unreachable in real execution, i.e., a false positive.

In abstract execution, we pick these properties beforehand in the form of the domain in which we want to compute. This domain then describes admissible abstract values. For example, to track the nullity of pointers, we may use a simple domain that consists of values: is zero, is nonzero, or is unknown (can be both zero or nonzero).

In general, we can look at both symbolic and abstract execution like they are performing an execution with sets of values instead of a single concrete value. For example, a nonzerovaluefrom a nullity abstract domain represents a set of integers {1, …, MAX_INT}, whereas the same set of values in the symbolic domain might be described as the expression x > 0.

What differentiates the abstract and symbolic execution from normal (concrete) execution is the ambiguity of control flow. Imagine you have a symbolic value v described by the expression x > 0. If this value is used in branch condition v > 10, both outcomes are admissible, either v > 10 or v <= 10. To deal with this situation, a symbolic executor needs to explore both paths separately.

Compilation-based approach

In computer-aided verification, most of the tools leverage abstraction techniques to reduce the complexity of analyzed systems. Even though these techniques are widely adopted, they are usually tightly integrated into tools: abstract semantics are an internal part of interpreters. This causes undesired complexity and neglects any reusable design. In my research, I devise a self-contained alternative to perform previously described abstractions independently of the tool. This self-contained approach is called compilation-based abstraction.

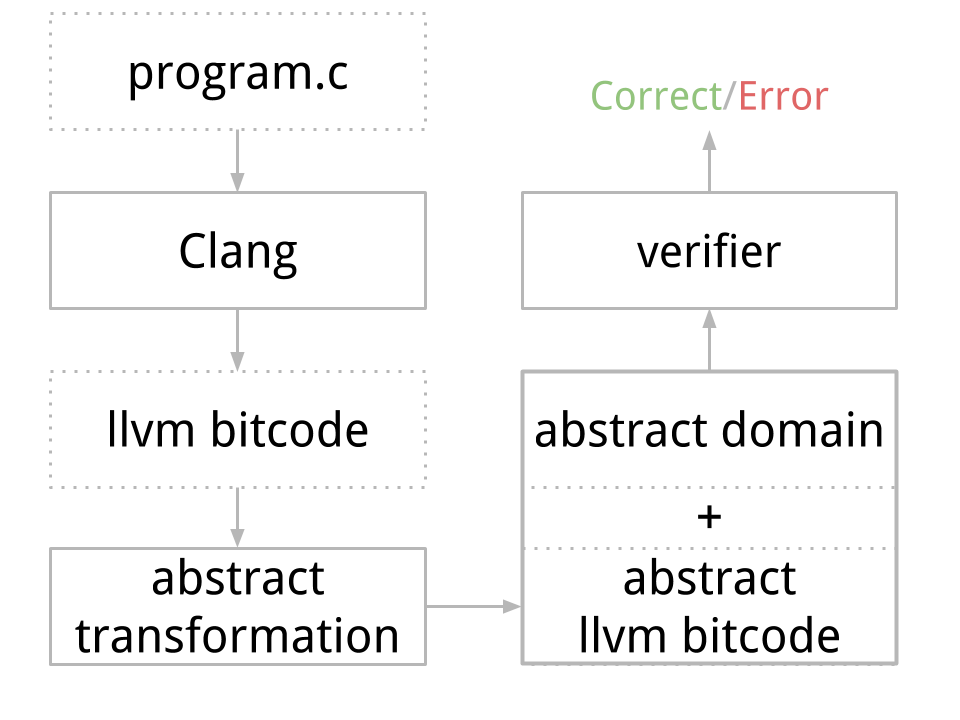
In the traditional approach, the abstraction execution is implemented in the interpreter. As you might guess, the compilation-based approach performs the abstraction before the actual analysis, during compilation. In short, the abstract compilation transforms program instructions that operate with user inputs to work with abstract representation instead, such as symbolic expressions. Once the program has been transformed in this way, it can then be analyzed by an arbitrary verification tool. The only requirement is that the tool (interpreter) can explore ambiguous branching because we do not know yet how to encode branching execution directly into the program simply. But in this way, the verification tool does not need to know about abstraction. In the big picture, the verification workflow with compilation-based abstraction looks like the diagram in Figure 3.

By comparison, the traditional workflow would implement and perform interpretation directly in the verifier. The compilation-based approach clearly offers some advantages. First of all, the simplified verifier is more efficient and more resilient to errors, giving us higher guarantees of the verification results. In fact, the verification also verifies the actual abstraction. On the other hand, the transformation increases the size of the analyzed code that needs to be interpreted, impacting the interpretation of the bitcode, which is, in consequence, slower than the direct implementation of abstraction in the verifier.

The solution I propose is implemented on the level of LLVM bitcode, which is simpler for analysis and transformation than the original C/C++ code. I have prototyped a solution in the DIVINE verifier. It is able to interpret LLVM bitcode and explorer branching executions. However, before integrating the compilation-based method, DIVINE could not process programs that take user inputs. The part of DIVINE that performs transformation is called LART: LLVM Abstraction and Refinement Tool.

Building a value abstraction

One of the design goals for compilation-based abstraction is to be accessible for developers, so that it is easy to create its own value abstractions. This is mainly achieved by implementing the actual abstract domain as a C++ library. To show you the ease of domain creation, let us now implement the previously mentioned nullity tracking domain, also called zero domain.

The implementation of an abstract domain is realized as a C++ class that defines how abstract values are represented and provides available operations on this representation. In the case of the zero domain, the representation is particularly simple: each value just maintains the information about its nullity.  We represent the nullity information with a single enumeration of possible value states:

struct zero_domain {
  enum value {
    zero,
    nonzero,
    unknown
  };
  

  …

The value can be either zero, nonzero, or unknown if the nullity is undetermined. An abstract value in the program can then be created either by an abstract input function that simulates an arbitrary input from the environment, or by lifting a concrete value:

value input() {
  return value::unknown;
}

value lift(int i) {
  if (i == 0)
    return value::zero;
  return value::nonzero;
}

Given this value representation, the domain then defines arithmetic operations:

value add(value a, value b) {
  if (a == value::zero)
    return b;
  if (b == value::zero)
    return a;
  return value::unknown;
}

For example, in the addition, we check whether one of the arguments is zero. In such a case, the result is the other value because the addition of zero does not change the result. In other cases, the result can be anything (an unknown value) since the addition of two nonzero values can result in both zero or nonzero due to integer overflow. The addition to unknown value is also undetermined.

Besides arithmetic operations, the abstract domain also needs to implement relational operations. For example, an equality operation (eq) in the zero domain can be implemented as in the following snippet. Note, we keep the semantics of the C language, where integer values also represent boolean values, so the result of comparison in the zero domain would also be a value in the zero domain.

value eq(value a, value b) {
  if (a == value::zero) {
    if (b == value::zero)
      return value::nonzero; // true
    if (b == value::nonzero)
      return value::zero; // false
  } else if (b == value::zero) {
    if (a == value::zero)
      return value::nonzero; // true
    if (a == value::nonzero)
      return value::zero; // false
  }
  return value::unknown;
}

The comparison is ambiguous (unknown) in the case when we compare two nonzero values; the abstraction is too coarse to determine equality of nonzero values. In the case when a program is to perform a branch based on an unknown value, we need to split execution and examine both paths, as shown in the introductory example.

Abstractions of data structures

Besides numeric values, we often manipulate programs with more complex data: arrays, strings, and other data structures. These are also interesting candidates for abstraction since many of those can come from the environment, and we want to explore multiple executions at once. The abstraction of data structures does not principally differ from numeric abstraction. In the domain, you describe an abstract representation of a data structure and implement its operations.

An example of such an abstraction would be a string abstraction suited for the verification of C programs, which I have developed during my research. This particular abstraction allows us to represent infinitely long strings with abstract characters as well. It is designed to repurpose numerical domains to represent characters and the length of strings. Moreover, the abstraction leverages the fact that the compilation-based approach can also abstract whole functions. Hence the string domain may provide its efficient abstract implementation of standard C library functions like strcmp, strcpy, etc.

Bitcode transformation also has uses beyond value abstraction. It provides the capability to perform arbitrary computation on the execution of instructions and functions. For example, one can implement statistical analyses that count the number of executions of particular instructions. Furthermore, the domain operations can check for specific properties during runtime. For example, we can utilize the transformation for security analyses and check whether some user input is used in a forbidden computation (e.g., memory manipulation).

Current research

As many abstract domains are imprecise, my current research focuses on domain refinement. The general idea behind domain refinement is to detect whether the found error is a false positive. In that case, the abstraction has to be augmented to forbid a particular error location’s reachability. In a compilation-based approach, this can be done with a simple swap of the abstract domain; the transformation does not need to be repeated. The only thing we need to do is to link new semantics (domain) and rerun the verification.

The other portion of my research focuses on the integration of multiple domains in a single program. This is a particularly challenging problem, where one needs to solve what to do when values from different domains come as arguments to a single operation.

The implementation of the transformation tool LART and domains presented in this article are currently a part of the verification framework DIVINE: divine.fi.muni.cz. However, there is also a work in progress on a standalone implementation at my GitHub repository: github.com/xlauko/lart.