If safety-critical systems fail, they can cause significant damage, including loss of life. In this article we consider methods to verify their behavior in production.

This is the second of a series of three articles about the formal analysis and verification of the real-time Linux kernel. Read the first article in RHRQ 2.3.

The challenge to enabling Linux in safety-critical applications is the requirement for a new set of tools that can demonstrate evidence that the system can achieve some level of safety. For instance, for time-sensitive systems  we would want to see a collection of evidence demonstrating that real-time capabilities need to be provided. Such a level of evidence depends on the criticality of the system, and it can range from continuous testing and documentation to the application of formal methods, the latter being the most sophisticated approach.

Formal methods consist of a collection of mathematical techniques to rigorously state the specifications of a system. The advantage of using mathematical notation is that it removes the ambiguous nature of natural language. The mathematical notation also enables the automatic verification of the system. Despite the arguments in favor of formal methods, its application is generally restricted to specific sectors. The most commonly mentioned reasons for that are the complexity of the mathematical notation used in the specifications and the limitations of computational space and processing time required to verify a system using formal methods.

In our previous article, we presented a formal specification approach using automata-based models, showing that it was possible to build a formal model of thread synchronization for the real-time Linux kernel. The final model accounted for more than 9,000 states and 21,000 transitions. However, it was built from reasonably small specifications, which made it practical for modeling purposes. We then need to ask: How to take benefits from the model? How can we check if the system adheres to the model?

Moreover, for safety-critical applications, it is as important to demonstrate the properties of the system as it is to provide ways for the system to react gracefully to a failure. For example, we can make the system fall back to a fail-safe mode in the case of detected misbehavior. Hence, to be effective, the usage of the formal methods must also allow the runtime verification of the system.

In this article, we will summarize the results presented in the paper “Efficient formal verification for the Linux kernel.” The paper proposed an efficient automata-based verification method for the Linux kernel, capable of verifying the correct sequences of in-kernel events at runtime. The method auto-generates C code from models, with efficient transition look-up time in O(1) for each hit event. The generated code can be then loaded on the fly into the kernel and dynamically associated with kernel-tracing events. This approach enables efficient runtime verification of the observed in-kernel events, as demonstrated in the next sections.

The efficient verification approach

The verification approach is presented in Figure 1:

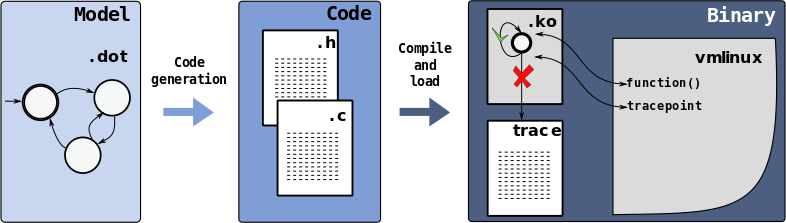
The verification approach has three major phases: the modeling phase, the model-code transformation phase, and the runtime verification phase.

The modeling phase
First, an automata-based model of Linux’s behavior is developed using the set of events available in the tracing infrastructure of Linux. (This modeling approach was presented in the first article of this series.) The model is represented using the Graphviz.dot open format. This format is widely used for automata models and can be exported from modeling tools such as Supremica.

The model-code generation phase
The automata formalism is better known by its graphical representation, as shown in Figure 2:

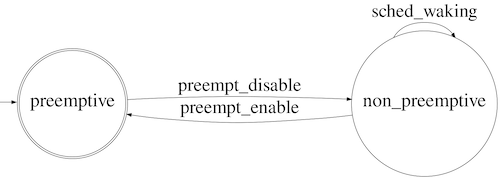
However, as the name suggests, the graphical format is just a representation of an automaton. A deterministic automaton, denoted by G, is actually formally defined by a tuple G = {X, E, f, x₀, X_m}, where

– X is the set of states;
– E is the finite set of events;
– f: X × E γ X is the transition function that defines the state transition in the occurrence of an event from E in the state X;
– x₀ is the initial state;
– X_m ⊆ X is the set of marked states.

The automaton works as follows. It starts at the initial state x₀, and upon the occurrence of an event e ⊆ E with f(x₀, e) defined, the state transition from x₀ to f(x₀, e) will take place. This process continues based on the transitions for which f is defined.

Exploring the formal representation, we developed a tool named dot2c. This dot2c translates the automaton in the .dot file into a C data structure. The auto-generated code follows a naming convention that allows it to be linked with a kernel module skeleton that is already able to refer to the generated data structures, performing the verification of occurring events. 

Regarding scalability, although the matrix is not the most efficient solution with respect to the memory footprint, in practice, the values are reasonable for nowadays common computing platforms. For instance, the Linux Task Model Automata presented in the previous article, with 9,017 states and 20,103 transitions, resulted in a binary object of less than 800KB, a reasonable value even for current Linux-based embedded systems.

The benefits of the format come in the runtime complexity/overhead. For example, the transition function f in C, shown in Figure 4, returns the next state in constant time O(1). The same complexity repeats for the other automaton operations in C.

The runtime verification phase
With the code generated from the model, the next challenge was to connect the verification code with the respective kernel events. Linux has an advanced set of tracing features, which are accessed mainly via perf and ftrace. Both other tools can hook to the in-kernel trace methods, processing the events in many different ways. The most common action is recording events into a trace buffer for post-processing or human interpretation of the events. However, it is also possible to hook other functions to trace events. For example, the live patching feature of Linux uses the function tracer to hook and deviate a problematic function to a revised version of the function that fixes a problem.

Exploring the possibility of hooking functions to the trace events, we proposed hooking the functions that run the automaton to the kernel events, enabling the online synchronous verification of the kernel.In this way, anytime a kernel event is generated, the function that parses the automaton is called, verifying if the model accepts the occurrence of that event. If the event is expected, it can be either logged or ignored. Otherwise, actions can be taken, ranging from the log of the exception to the halt of the system, to avoid the propagation of a failure.

Hence, the verification mechanism has a two-fold contribution to the application of Linux on safety-critical systems: it enables the continuous verification of the kernel against formal specifications, and it allows prompt reactions to the occurrence of unexpected events.

However, to be practical, the overhead of the verification needs to be acceptable for production systems. This aspect is explored in the next section.

Performance analysis

We demonstrated the performance of the proposed technique by presenting evaluation results on a real platform, verifying models in terms of the two most important performance metrics for Linux developers: throughput and latency.

The measurements were conducted on an HP ProLiant BL460c G7 server, with two six-core Intel Xeon L5640 processors and 12GB of RAM, running a Fedora 30 Linux distribution. The kernel selected for the experiments is the Linux PREEMPT_RT version 5.0.7-rt5.

Throughput evaluation was made using the Phoronix Test Suite benchmark, and its output is shown in Figure 5. The same experiments were repeated in three different configurations:

1. The benchmark was run in the system as-is, without any tracing or verification running.
2. It was run in the system after enabling verification of the SWA model.
3. A run was made with the system being traced, only limited to the events used in the verified automaton.

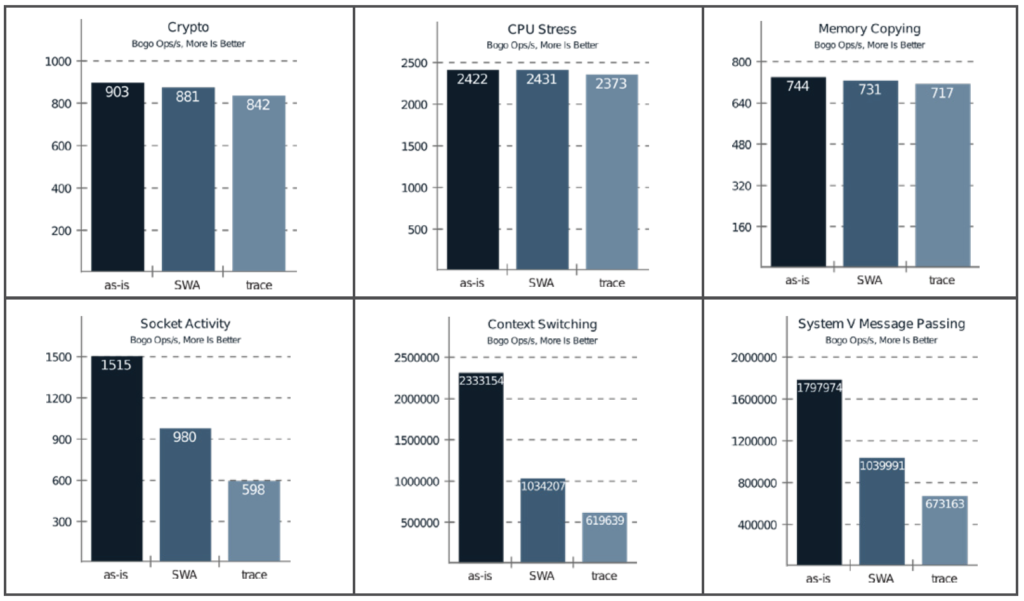
It is worth mentioning that tracing in the experiments means only recording the events. The complete verification in user space would still require the copy of data to user space and the verification itself, which would add further overhead.

On the CPU bound tests (Crypto, CPU Stress, and Memory Copying), both trace and verification have a low impact on the system performance. In contrast, the benchmarks that run mostly on kernel code highlight the overheads of both methods. In all cases, the verification performs better than tracing. Despite the efficiency of tracing, the amount of data that has to be manipulated costs more than the simple operations required to do the verification, essentially the cost of looking up the next state in memory in O(1), and storing the next state with a single memory write operation.

Latency is the main metric used when working with the PREEMPT_RT kernel. The latency of interest is defined as the delay that the highest real-time priority thread suffers during a new activation due to in-kernel synchronization. Linux practitioners use the cyclictest tool to measure this latency and rteval as background workload, generating intensive kernel activation. Like the previous experiment, the verification of a model (the NRS model in this case) was evaluated against the kernel as-is, with the kernel merely tracing the same set of events. Consistent with the results obtained in the throughput experiments, the proposed verification mechanism is more efficient than the sole tracing of the same events while keeping the overhead low.

Final remarks

In the previous article, we showed that it is possible to model Linux’s complex behavior using automata-based specifications. However, that work would not be practical without a way to verify that the kernel and the model adhere to each other. In this article, we present an approach that makes the runtime verification of the Linux kernel feasible. We achieved this result by reducing the complexity of transforming a model into code with automatic code generation and by leveraging the Linux tracing features to enable the kernel’s online verification. The performance results confirmed that the automata’s simple format translates into fast verification operations, allowing the verification of the system in production. Moreover, the ability to take action on the occurrence of unexpected events is a crucial technology to enable Linux’s usage on safety-critical systems, increasing the need for such verification methods on Linux.

Additionally, we showed in the first article how to formalize the specifications of the real-time Linux kernel. Here, we have shown how to verify these specifications efficiently. With these results, we achieved the goal of ascertaining the logical behavior of the essential synchronization of the real-time kernel. However, the correctness of real-time systems does not depend only on the system’s logical behavior but also on the timing behavior. The next article in this series will discuss how to leverage the model to extract a sound bound for the primary real-time Linux metric, the scheduling latency.

This article is a summary of the paper Daniel Bristot de Oliveira, Tommaso Cucinotta, and Rômulo Silva de Oliveira, “Efficient formal verification for the Linux kernel,” International Conference on Software Engineering and Formal Methods (Cham: Springer, 2019).