Timing attacks have been used successfully against a variety of popular encryption techniques, but they can be prevented with consistent use of constant-time code practice.

Cryptography provides privacy for millions of people, whether by ensuring end-to-end encrypted messaging, securing more than ninety percent of the web behind HTTPS, or establishing trust behind the digital signatures used in electronic ID cards. And all of this cryptography needs to be implemented somewhere, by someone. 

In the case of HTTPS, encryption is usually done in open source cryptographic TLS libraries such as OpenSSL, which is used by most web servers in internet-wide scans. Other implementations, however, are closed source. For example, the smartcards used by electronic IDs are done by the vendors of the cryptographic hardware. These libraries and smartcards have suffered serious vulnerabilities in the past, mostly coming from memory safety or logic issues, but some vulnerabilities will be found not in the code, but in its outside behavior.

All code, including cryptographic code, has to be executed on actual physical hardware. This execution takes some amount of time, uses some amount of power, might produce results and errors, and, like any electrical device, it emits a small amount of electromagnetic radiation and heat. All of these results of the execution depend, in one way or another, on the code that was executed and the data that the code used. The timing dependency on code executed is clear: executing instructions on a processor as well as accessing memory takes time. The code can also branch on data and thus execute different instructions, which will result in a dependency between execution time and data. 

Modern processors have caches that store values recently used from memory for very fast access, with the idea that recently used memory addresses will be used again. Caches provide fast memory access only if the read address is present in them (a cache hit) and provide no speedup on a missing address (cache miss). This leads to some interesting behavior: the same sequence of instructions accessing the same memory addresses can take different execution times, depending on the state of the caches. 

Digging deeper into how the logic gates and transistors in modern processors work reveals the dependency between code/data and power consumed by a device. Logic gates consume different amounts of power when their output changes versus when it stays constant. This changing power consumption directly leads to the dependency of power—as well as electromagnetic radiation and heat—on the executed code and data.

The physical and temporal effects of computation, usually called side-channels, are clearly established. However, we also need to know whether they can impact security. Do we need to care about side-channels? Do we need to avoid them completely or at least minimize them? 

These questions were answered twenty-five years ago in a seminal paper by Paul Kocher, which introduced the concept of timing attacks.¹ In a timing attack, the attacker extracts secret information by measuring the execution time of a cryptographic function operating on secret keys or information.

A piece of code leaks secrets through a timing leak if it conditionally branches on secret values or accesses memory based on secret values. Kocher presented attacks on example implementations of several then-popular cryptosystems, such as Diffie-Hellman, Rivest–Shamir–Adleman (RSA), and Digital Signature Standard (DSS), variants of which are still used and attacked today. Timing attacks require that the attacker can measure the runtime of a sensitive operation, function, or call with some precision. The required precision and amount of measurements vary significantly based on the size of the timing leak and noise.

A simple example of code vulnerable to a timing attack is displayed in Figure 1. Try to see for yourself how this code could be vulnerable, assuming that you as an attacker can trigger the check_password function with any input password and can measure its execution time precisely. The goal is, of course, to obtain the correct password embedded in the function, ignoring for a moment that passwords should be stored hashed with salt and pepper and not hardcoded. Stop and don’t read further if you want to find the attack yourself, as its description follows. 

The attack is an iterative one and is based on the fact that the early return in the for loop terminates the execution of the function at the first character of the input password that is different from the correct password. This allows the attacker to guess the password character by character from its beginning, trying “A_,” “B_,” etc., which will take a similar amount of time, until “H_” takes longer. 

It might be surprising, but very similar attacks were used to target many popular crypto implementations, including some recent implementations of post-quantum cryptography.² Their target was the memcmp function, which is used to compare buffers of data. Memcmp needs to be fast and thus similarly aborts the comparison as soon as it finds a difference. The attacker can then gain rough information about how many bytes were equal, which can be used to brute force a value compared against an attacker-controlled one. This was enough to mount a serious attack on several cryptosystem implementations that hope to win a competition of cryptosystems for a future world with quantum computers.

The Minerva attack

Our research first seriously dived into timing attacks with the Minerva group of vulnerabilities in the Elliptic Curve Digital Signature Algorithm (ECDSA). Elliptic curves are mathematical objects with rich properties that happen to be very well suited for building cryptography. Roughly speaking, an elliptic curve is a set of points on a plane, the coordinates of which satisfy an equation of the form y²= x³ +ax +b. There is a very natural way to add points on the curve and obtain another point on the curve, in the same way that adding integers produces another integer. On elliptic curves, adding the same point to itself many times (i.e., multiplication) is called scalar multiplication to signify that one is multiplying the point with a scalar. 

The similarities with the addition of integers end here. It is easy to invert integer multiplication by simply dividing with the integer multiplicand and obtaining the multiplier. However, inverting scalar multiplication on well-chosen elliptic curves—that is, computing the scalar used to multiply a point given the point and its multiple—is a hard problem for which there are no practical algorithms known. This hard problem forms the basis of elliptic curve cryptography and the ECDSA cryptosystem.

ECDSA is a digital signature algorithm. When a signer signs a message (a document, for example), they need, or rather their cryptographic implementation needs, to pick a random integer called a nonce. It then performs scalar multiplication of a given fixed point with this nonce as the scalar, using the result in some further computations to produce the signature. The nonce needs to be uniformly random in a given fixed range and can never be revealed to the attacker or reused. Doing so would lead to a complete break of the cryptosystem, giving the attacker the capability to forge signatures. Even giving partial information about many used nonces to the attacker can have catastrophic consequences, as attacks using lattices can extract the private signing key and break the cryptosystem.

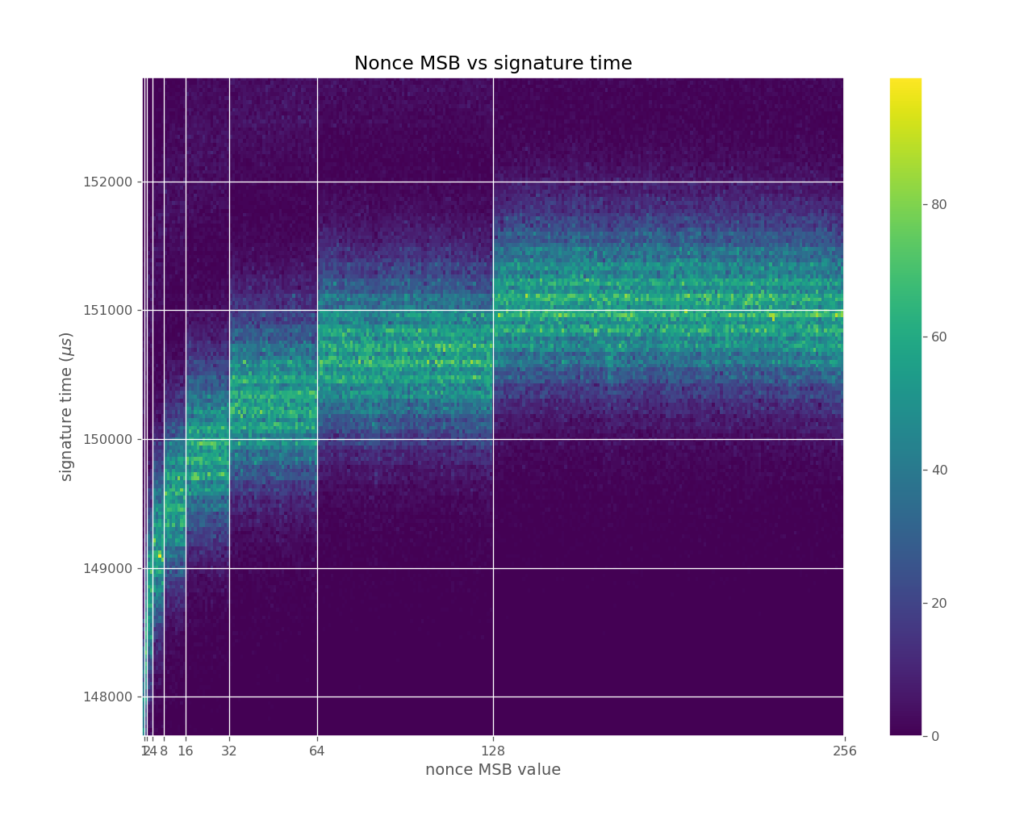
We discovered the first vulnerability that would come to be in the Minerva group of vulnerabilities while working on ECTester, a tool for testing black-box elliptic curve implementations in smartcards and software libraries. We first noticed an issue in a quick Python Matplotlib heatmap of the most significant byte of the random nonce and the runtime of ECDSA signing on the Athena IDProtect smartcard, which is displayed in Figure 2. If there were no timing leak, the figure would look like a horizontal line, showing no relationship between execution time and the value of the secret random nonce. However, the ECDSA implementation on the Athena smartcard was leaking the bit length of the random nonce linearly; that is, each additional bit in the binary representation of the random nonce added some processing time, which is visible in the figure as distinct steps at the powers of two values. With each measured ECDSA signing, the attacker thus gains noisy information on the bit length of the random nonce used in the signature. 

Is this enough for an attack, given that the common ECDSA private key has 256 random bits and thus is uniformly distributed among 2²⁵⁶ values? Luckily for the attacker, knowledge of the bit length can be turned to knowledge of the most significant bits of the random nonce (small bit length means that topmost bits are zero), and then a lattice attack can be used to extract the private key given enough measured signatures. We demonstrated this attack on the Athena IDProtect, which was both Common Criteria and FIPS 140-2 certified, and also enhanced the attack method significantly. After extending our data collection to include open source cryptographic software libraries, we found five more libraries with the same timing leak. Similar leakage was found in a certified Trusted Platform Chip by a subsequent paper.

Defending against timing attacks

What could the vulnerable implementations have done to prevent leaking sensitive information through a timing leak? The most common countermeasure against timing attacks is to develop sensitive cryptographic code with constant-time code practice. That is, to develop code such that:

• There is no information flow from secrets to branch conditions or loop bounds.
• Addresses used for memory access are not influenced by secret data.
• Secret data is not given as arguments to some instructions that might execute in variable time.

Following the above rules ensures that even an attacker who can measure the execution of the sensitive code and observe its memory accesses will not be able to gain any information about the secrets used. Some algorithms, like those for scalar multiplication on an elliptic curve, have versions that are naturally constant-time (i.e., that satisfy the above conditions, thus are safe from timing attacks). Other countermeasures against timing attacks exist, for example, blinding, which randomizes values used inside the computation to make the leak useless. However, the constant-time code practice remains the most frequently used. 

There is one significant issue with ensuring that code is constant-time while reasoning about it on a source code level, namely the compiler. Recent research has shown that modern optimizing compilers can easily take code that looks constant-time and produce a binary that is leaking. Developers thus often need to trick the compiler into not introducing these issues in their code.

If trusting developers to follow secure programming guidelines, including the constant-time rules, were enough, there would be no bugs or vulnerabilities in any code. As all humans make mistakes, we should not leave them alone, fighting in the trenches, but provide tooling that will help them make their code constant-time or test whether it is constant-time, similar to how testing and fuzzing are used to help ensure code correctness. Luckily, such tools already exist. In fact, a recent analysis of the landscape found over thirty of them. The tools range in functionality and approach: some take code and transform it into constant-time code, while others verify that existing code or binary is constant-time. Some tools use a formal approach and are sound, meaning that there is proof that they will find all timing leaks in the code.

Why are timing attacks still around?

Given that there are effective countermeasures, techniques, and tools for verification of resistance to timing attacks, why are there still new timing attacks? To begin answering the question, we can look at the use of tools for verifying resistance to timing attacks. While eleven out of fifteen popular cryptographic libraries test the correctness of their code in their continuous integration (CI) pipelines, only four of them use the tools to verify resistance against timing attacks in their CI. Why are these tools not widely used? Is it that developers don’t know about them? Or is it the typically poor usability of tools that are mainly research artifacts and not ready-to-use products? We hope to answer all of these questions in our research. 

To do so, we decided to ask the developers directly by conducting a survey with developers of prominent open source cryptographic libraries in cooperation with researchers from Max Planck Institute for Security and Privacy in Bochum, Germany, and the University of Rennes, France. The survey concluded with forty-four developers from twenty-seven libraries participating and sharing their knowledge and opinions on timing attacks, countermeasures, and tools. We hope that this study gives us interesting insights into developers’ views towards timing attacks—and that we can move from arguing about timing attacks using anecdotal evidence to discussions based on proper results. Expect a paper with details soon.

Footnotes

 ¹ “Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems,” CRYPTO (1996).

² Qian Guo, Thomas Johansson, and Alexander Nilsson, “A key-recovery timing attack on post-quantum primitives using the Fujisaki-Okamoto transformation and its application on FrodoKEM,” Advances in Cryptology—CRYPTO 2020, pp. 359-86.