Passwords made are to be memorable, so they are not usually secure enough for encryption software. That’s where derivation functions come in, transforming a password into a more suitable cryptographic key. Memory-hard functions—functions that cost a significant amount of memory to evaluate—are especially useful to mitigate time-memory trade-off attacks. Here, we describe research on Argon2, one such memory-hard function.
…if these are the calculations that an attacker might make, what calculations should a defender be making?
This article summarizes my research while a master’s student at the Masaryk University Faculty of Informatics. I simulated an attack on a disk encrypted with the LUKS2 encryption scheme using Argon2, the 2015 winner of the Password Hashing Competition (password-hashing.net), as the password-based key derivation function (PBKDF). During this simulated attack, I collected Argon2 parameters benchmarked by Cryptsetup software. The attack simulation ran over both CPUs and GPUs and allowed me to estimate the costs to an attacker using either physical hardware or on-demand allocation of computing resources in the cloud.
The results were astonishing: it can take thousands of machines and hundreds of millions of dollars over ten years to crack an eight-character LUKS2 password using Argon2.
Passwords need to be resilient
Organizations are putting more pressure on all of us to create more secure passwords, but this is very difficult as they are usually not sufficiently long. They are composed of printable characters, thus they do not meet the requirement of being uniformly distributed. If a human should be able to remember them, they will probably contain dictionary words, which increases their discoverability even more. Running a password through a PBKDF derives one or more cryptographic keys from it. These derived keys are pseudorandom and sufficiently long to make brute-force guessing as time consuming as possible.
Lately PBKDFs are taking on another defensive role. Due to the availability of GPUs, FPGAs, and ASICs, there are new possibilities for running functions in parallel in computing environments, increasing the effectiveness of brute-force attacks. PBKDFs try to defend against such attacks by using memory-hard algorithms to slow down potential attackers and to make running the function in parallel extremely expensive or inefficient. To point out one example, cracking an eight-character passphrase used to unlock an encrypted volume in around two seconds on a Raspberry PI could take up to 1,085 NVIDIA Tesla P100 GPUs, costing about 120 million dollars. Trying to crack a volume encrypted with Argon2 created on a modern laptop would require up to 75,121 powerful machines running for ten years and cost over 4 billion dollars.
When the backup system needs a backup system
It did not take long for password crackers to get the better of PBKDF2 by finding weaknesses in their parallel computing and GPU optimization. The usual way of attacking is to use brute force to try as many variations of keys as possible, or to use a dictionary approach that assumes passwords are based on actual words. Memory-hard functions such as Argon2 were a mechanism for making the compute power required for these attacks simply too expensive or time consuming for the efforts to be worthwhile, except in the rarest of cases.
Even the protections offered by Argon2 were soon not enough, as a 2016 paper concludes (https://eprint.iacr.org/2016/759.pdf). Making multiple passes through the hashing algorithm became essential to protect a password: where 6 passes had at first been considered “paranoid,” 10 passes were now recommended.
Pricing the cost of a hack
Based on previous assumptions of an attacker’s options, I created a price model that would estimate costs connected with finding the right passphrase to unlock a LUKS2 encrypted volume. These costs include purchase of devices and electricity costs. The variables shown in Figure 1 were defined to formalize the model.
D– power draw of one machine expressed in kilowatts
E – price of electricity expressed in dollars per kilowatt hour
F – expected final price of whole attack expressed in dollars
H – initial price of one machine (CPU, RAM, accessories) expressed in dollars
L – expected length of an attack expressed in days
N – number of machines expressed as an integer
P – number of passwords contained in the chosen password space expressed as an integer
R – price to rent one machine for one hour expressed in dollars
S – speed of one machine expressed as number of seconds spent computing one hash
Figure 1. Variables in the password discover-cost formula
The model expects that an attacker uses an array of homogeneous machines and that the speed of Argon2 hash cracking is at least approximately benchmarked. It does not assume any hints about the password. It expects that passwords are distributed uniformly through the password space and therefore an attacker should on average search through one half of P to recover the password.
The model can simulate two different cases. In the first case, an attacker plans to purchase actual physical hardware, and, in the second case, an attacker rents machines from an online cloud provider (Amazon, Microsoft Azure, Alibaba Cloud, etc.). The final price is determined by the equations shown in Figure 2.
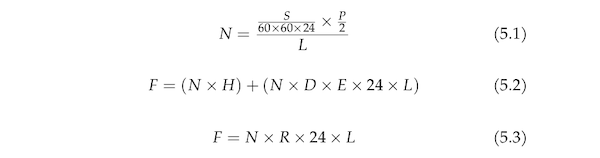
Figure 2. Equations for determining the cost of
password discovery
Equation 5.1 determines how many machines are needed to exhaust the complete password space P in L days. The result denoted as N can then be used in equations 5.2 or 5.3. Equation 5.2 is used in the case of purchasing and using physical hardware. In that case, an attacker could estimate the power draw of a single machine by collecting information from data sheets or by performing real world tests. There exist online versions of power consumption calculators. If an attacker decides to allocate computing resources in online clouds, then equation 5.3 should be used. Online cloud providers usually provide online price lists for their services.
The path forward
Where could this research lead next? The main method for simulating an attack against Argon2 was based on the Argon2-gpu-bench benchmarking tool. Only the computation of Argon2 is involved; no actual decryption of volumes is performed. It would be interesting to create a fully working cracking tool and test its performance, eventually making the price model more exact. This process could be connected with measuring the real power draw of physical machines while performing the attack. These values would make the model even more precise.
Another area for further research is using cloud-based computing services. The prices and estimates described in my thesis were made only based on theoretical information, and no actual computation was made using these resources. The real efficiency might differ, and in that case it might positively or negatively influence the resulting price and suitability for the attack.
One might wonder, if these are the calculations that an attacker might make, what calculations should a defender be making?
Acknowledgements

I would like to acknowledge the following support:
Computational resources were supplied by the Ministry of Education, Youth, and Sports of the Czech Republic under the Projects CESNET (Project No. LM2015042) and CERIT-Scientific Cloud (Project No. LM2015085) provided within the program Projects of Large Research, Development, and Innovations Infrastructures.
Additionally, thanks go to my advisor Milan Brož for very inspirational supervision and for help with gaining access to hardware needed for benchmarking. Furthermore, I would like to thank Ondrej Mosnáček for his consultations concerning Argon2 and for the software used in this thesis. The English version of the complete thesis is available at https://is.muni.cz/th/yinya/?lang=en.



